10 使用样例
样例要求MView版本>=0.4.3,对Gaussian、ORCA等计算软件版本无特定要求。
10.1 3-氯吡啶与 \(CO_{2}\) 的相互作用
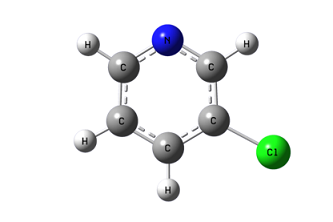
3-氯吡啶化学式为 \(C_{5}H_{4}NCl\) ,对应结构式如下图所示
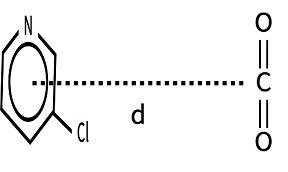
如下图所示,本例将 \(CO_{2}\) 置于吡啶环结构上方,并尝试使用Gaussian软件计算 \(CO_{2}\) 与3-氯吡啶距离 \(d\) 距离增大时体系的能量变化情况。
步骤如下:
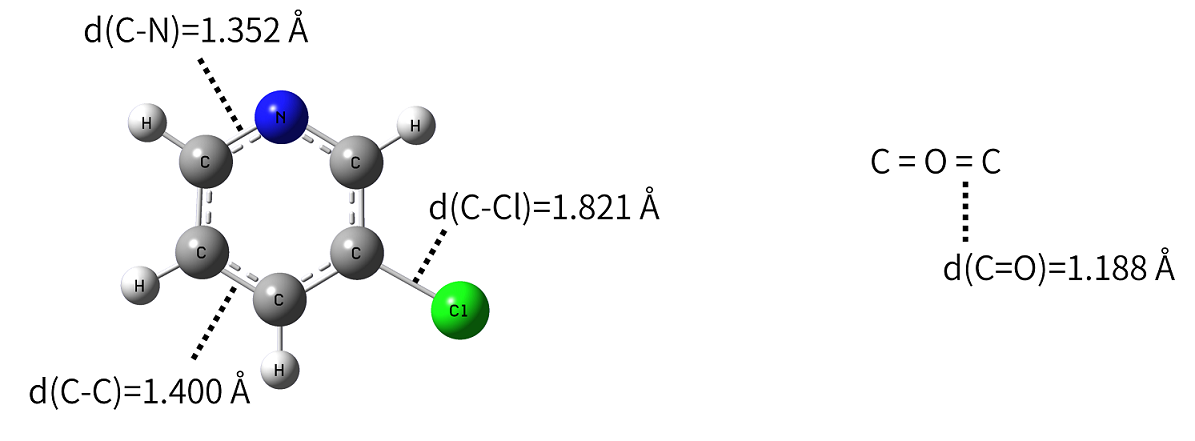
1. 构建3-氯吡啶与 \(CO_{2}\) 模型,并使用Gaussian软件分别对它们进行几何优化。作为样例,这里使用B3LYP/6-31G进行优化,优化完成后,两分子主要键长如下图所示。
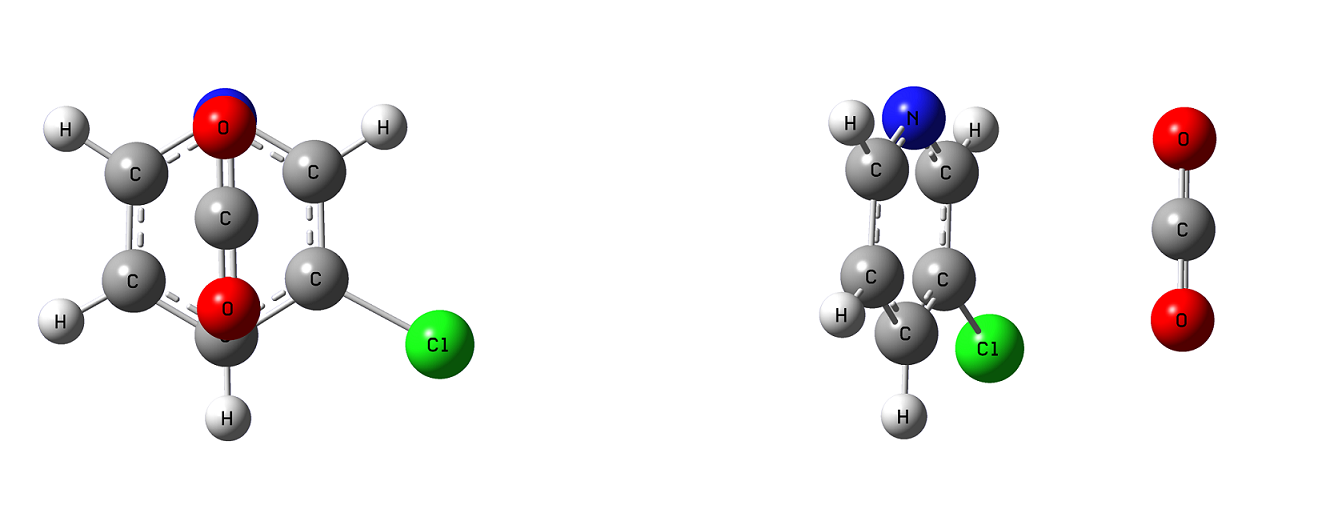
2. 在GaussView中新建一个窗口,将优化好的3-氯吡啶与 \(CO_{2}\) 分子分别复制粘贴到窗口中,这里将3-氯吡啶置于xy平面,并将 \(CO_{2}\) 分子置于3-氯吡啶的上方。实际上扫描过程中 \(CO_{2}\) 分子与3-氯吡啶的相对角度对扫描结果会有一定的影响,出于简化这里暂不考虑。
3. 将模型保存为.gjf文件,注意保存过程需要保留化学键信息。如果保存得到的结果没有化学键信息,可以在保存得到文件的计算任务栏中添加geom=connectivity关键字,再使用GaussView进行保存。
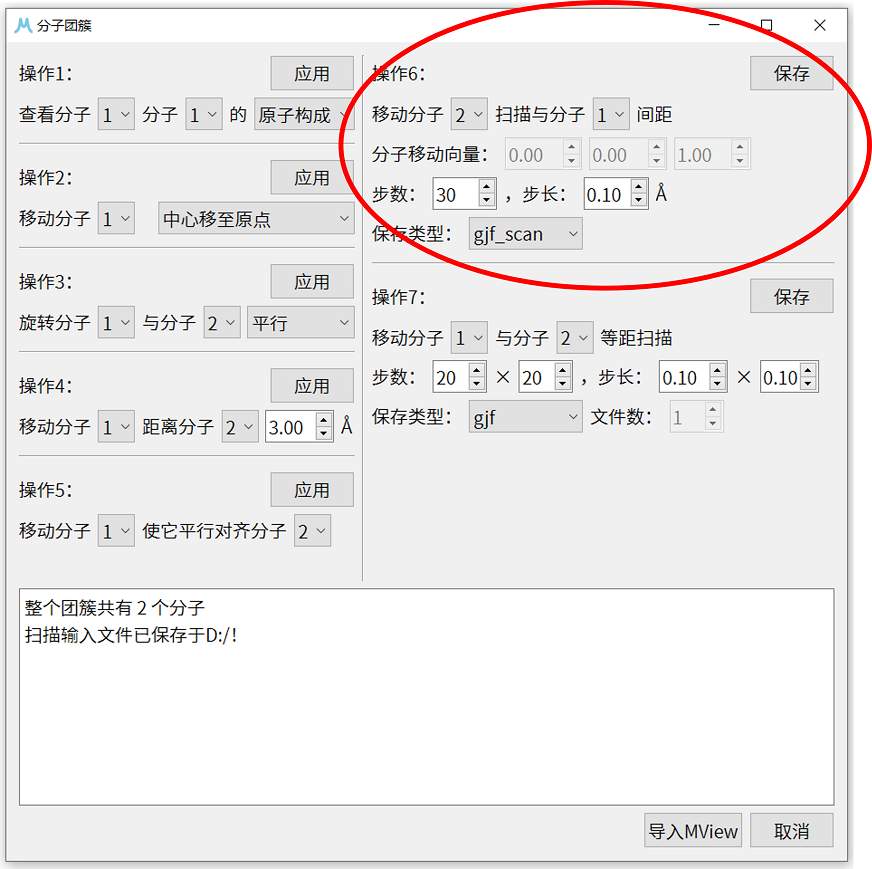
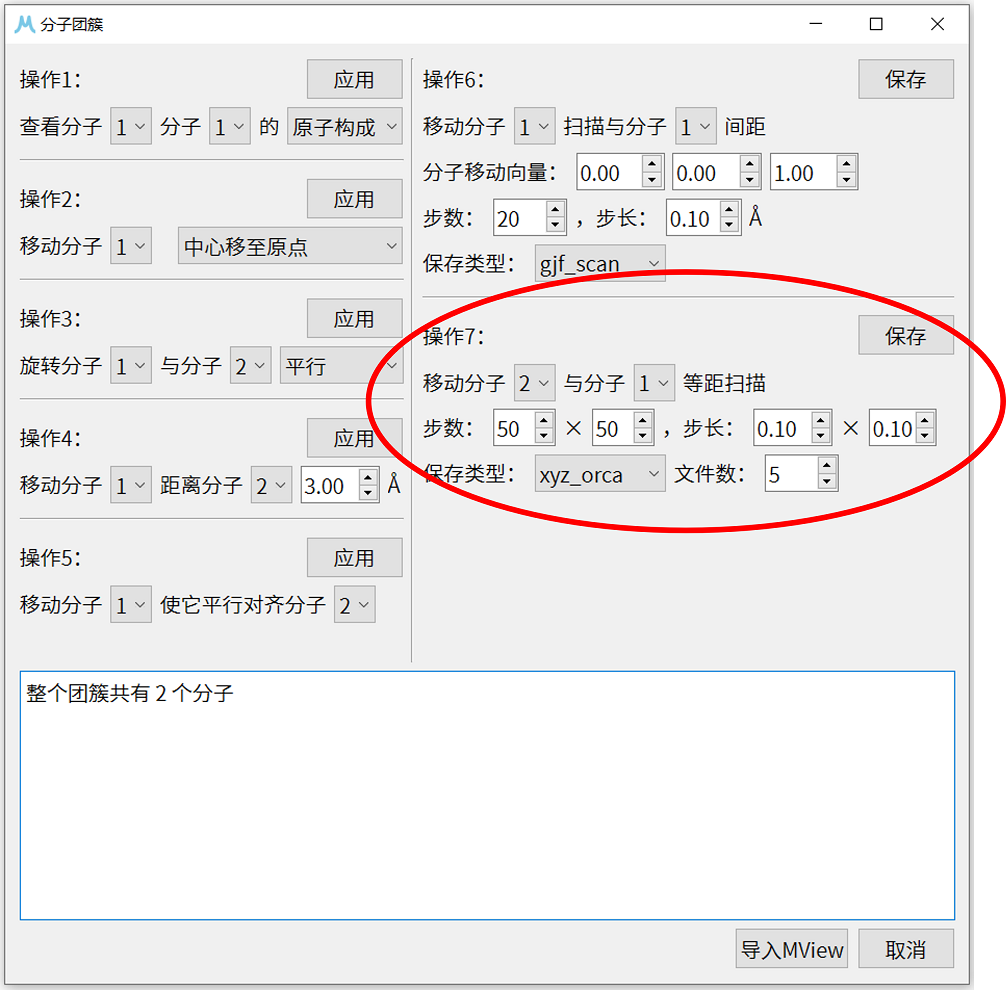
4. 使用MView打开得到的.gjf文件,点击左下方分子团簇按钮,打开分子团簇界面。
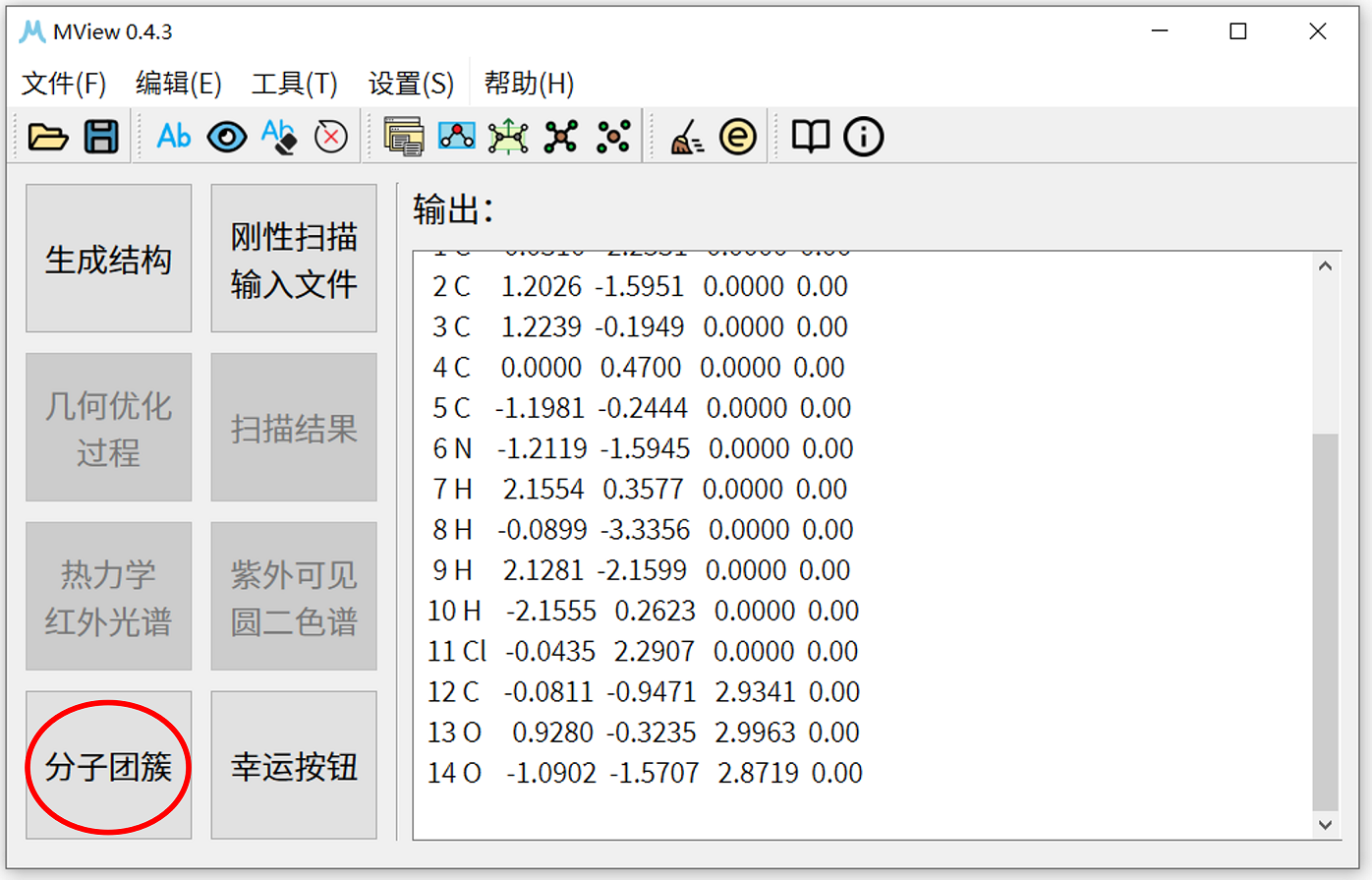
5. 这时可以单击操作1中应用按钮,查看分子团簇的组成与分子中心,可以看出在这里分子1是3-氯吡啶,几何中心为(0.1800,-0.7270,0.0000),分子2是 \(CO_{2}\) ,几何中心为(-0.0811,-0.9471,2.9341)。
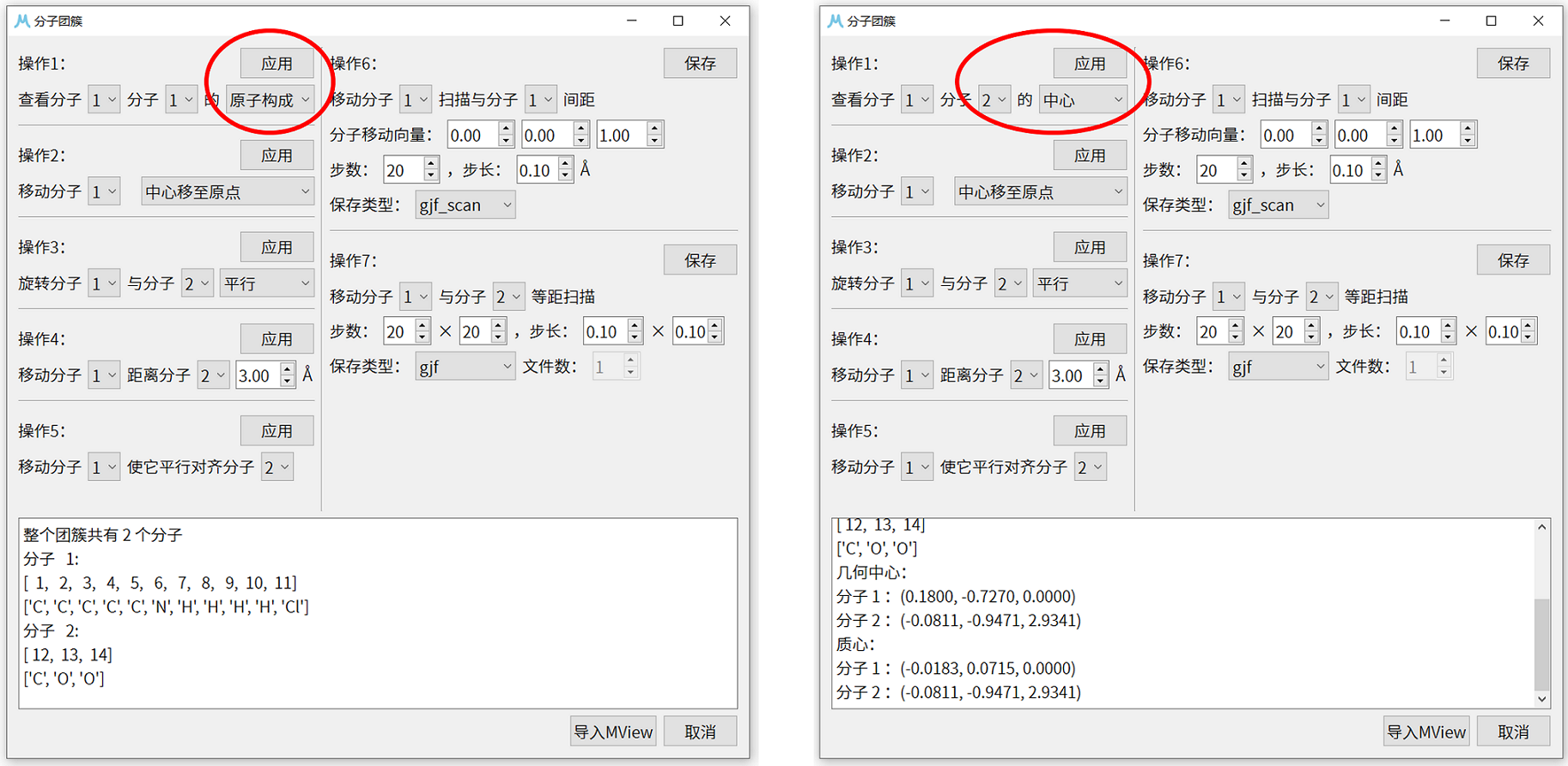
6. 本例打算扫描两分子距离在 3.0 Å至 6.0 Å下能量随距离的变化关系,因而需要将两分子中心的初始距离设置为 3.0 Å。首先利用操作2将分子1的中心移至原点,随后再将分子2的中心移至原点。
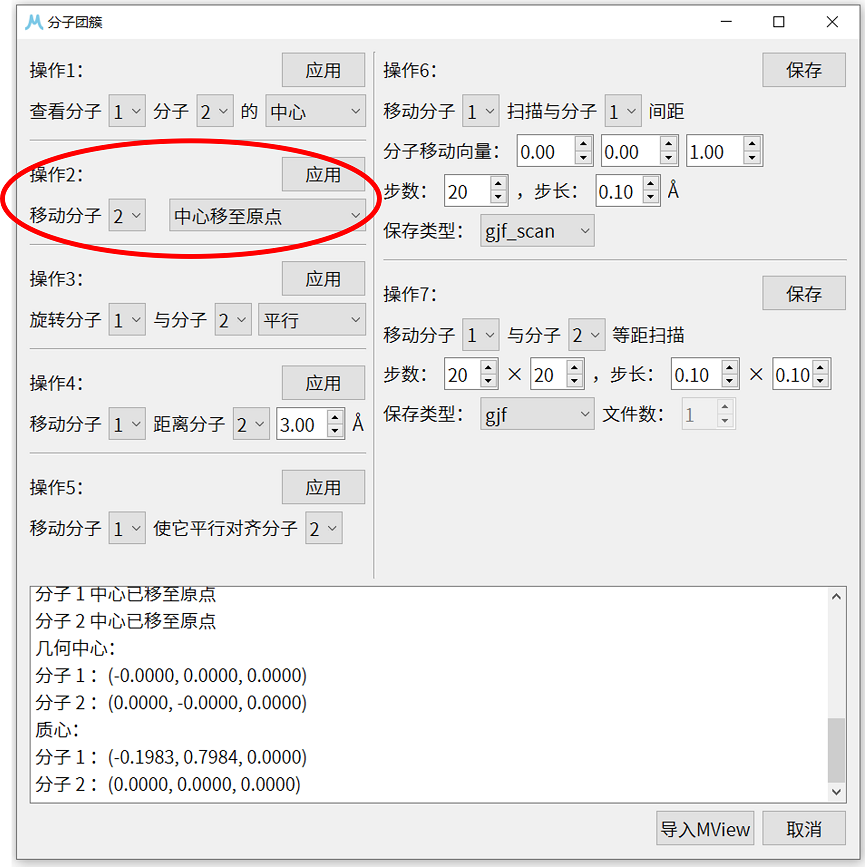
7. 使用操作4移动分子2( \(CO_{2}\) 分子),使其与分子1(3-氯吡啶分子)的距离为 3.0 Å。如果两个分子几何中心不重合,操作4会沿两分子几何中心连线调整分子距离,但这里两个分子几何中心重合,操作4会沿z轴向量(0,0,1)方向移动分子2。操作完成后,可以使用操作1确认 \(CO_{2}\) 分子的中心已被调整为(0.0000,0.0000,3.0000)。
8. 这里也可以使用图形可视化界面确认初始结构正确性,点击分子团簇界面右下角的导入MView按钮,并点击MView的显示分子按钮,即可调用MView外接的可视化工具查看目前的结构信息,下图的展示中外接的是Jmol。
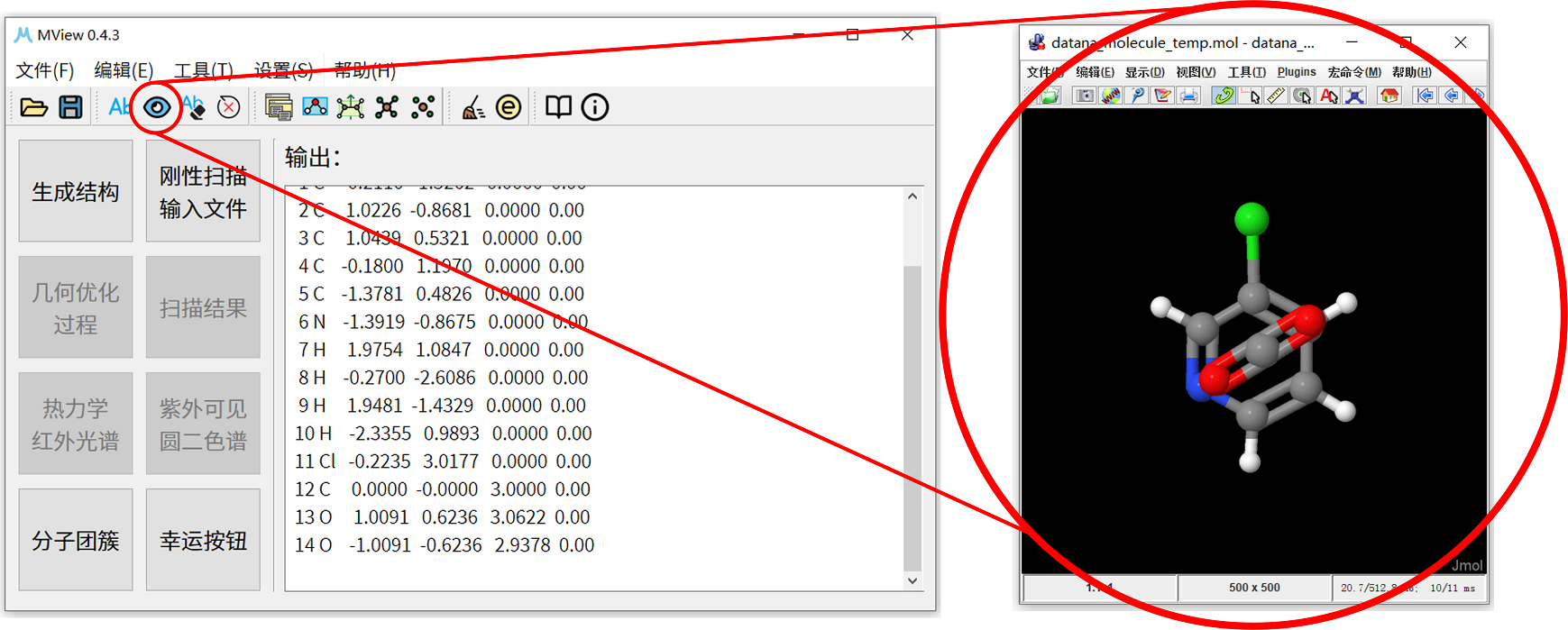
9. 关闭可视化工具,单击分子团簇重新打开分子团簇窗口。在操作6中,选择移动分子2,扫描步数设置为30,步长为 0.10 Å,保存类型选择gjf_scan。gjf_scan对应的是Gaussian的内坐标格式扫描文件。点击右上角保存,选择要保存的文件夹路径,注意此时不需要输入保存文件的文件名,保存成功后,对应保存路径下会生成名为scan_file_gaussian.gjf的文件。
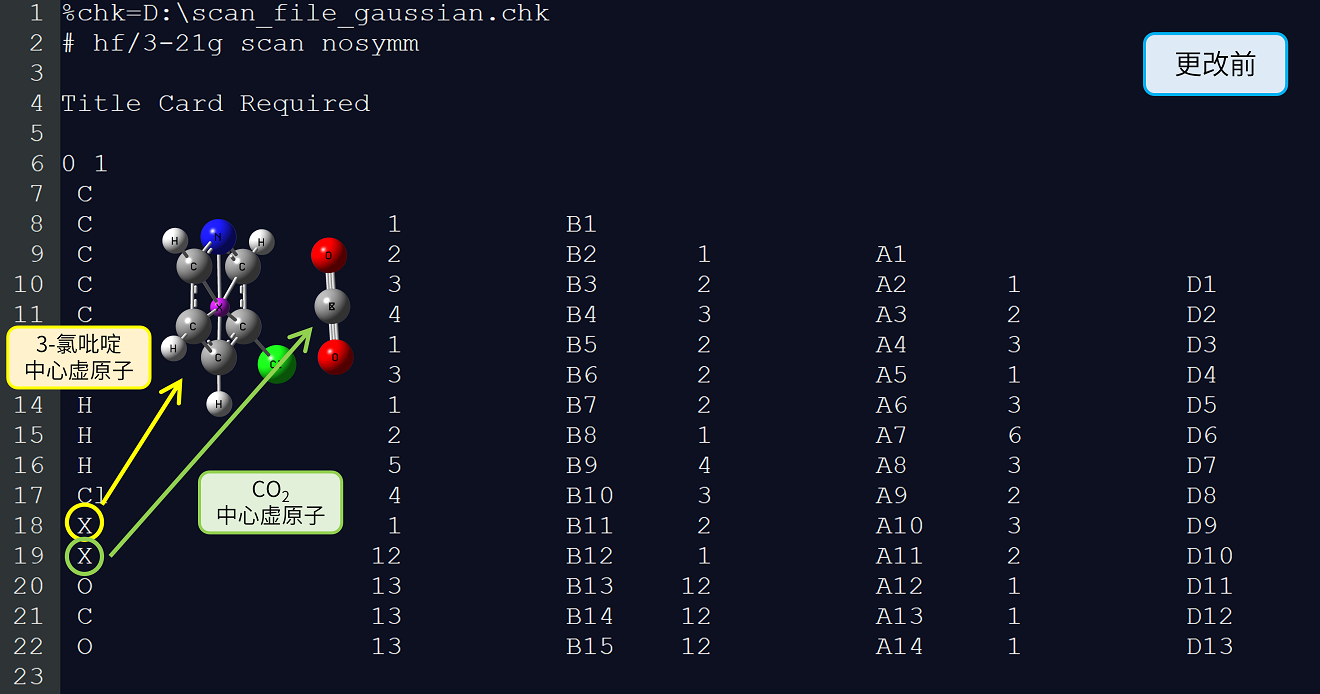
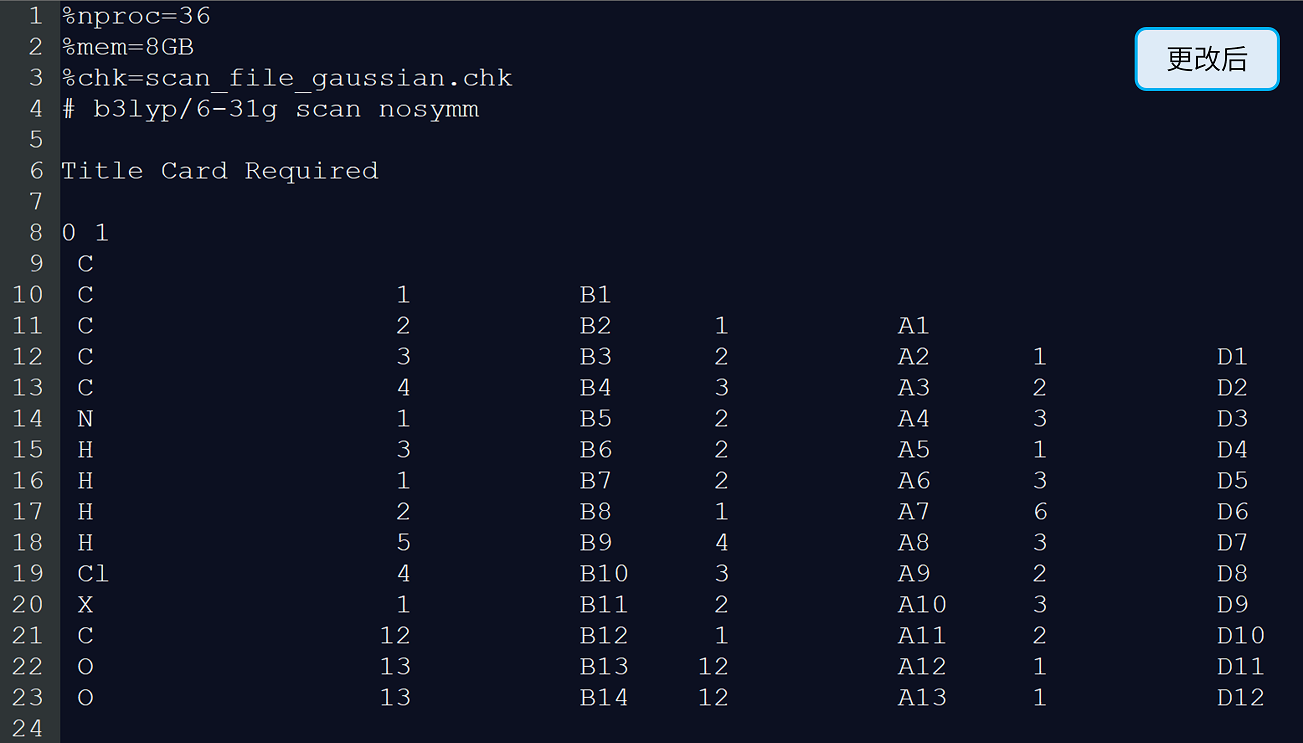
10. 打开scan_file_gaussian.gjf文件,可以看到扫描文件的构建方式是分别在两个分子中心添加了虚原子 \(X\) ,将两个分子键连至虚原子上,并扫描虚原子之间的距离。根据不同体系,可以对扫描文件做最后的微调。例如这里 \(CO_{2}\) 分子的C原子和虚原子重合,可以删除 \(CO_{2}\) 分子的虚原子,直接扫描 \(CO_{2}\) 的 \(C\) 原子与3-氯吡啶虚原子的距离。此外,还需要将扫描使用的方法更改为B3LYP/6-31G。
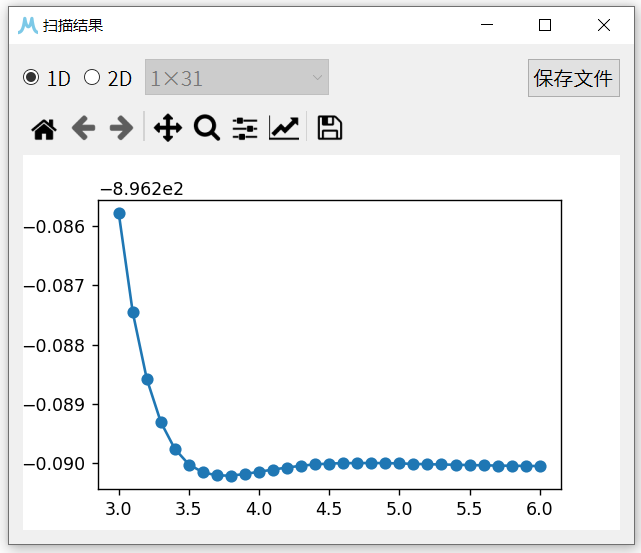
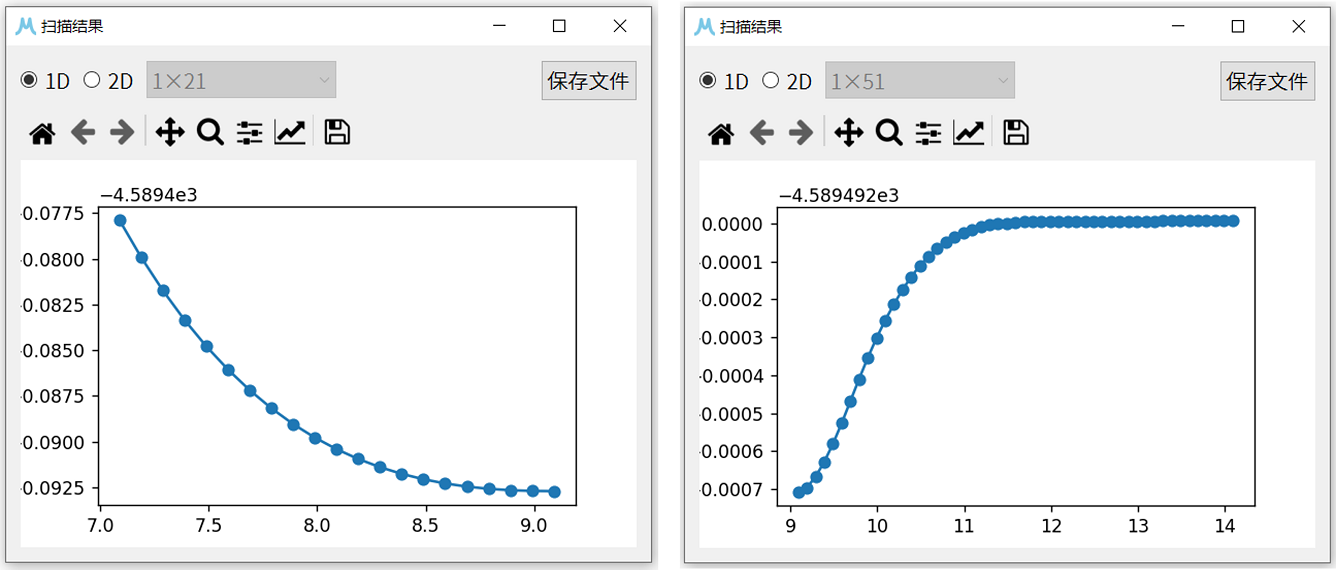
11. 使用Gaussian运行得到的输入文件,可得到对应的扫描结果scan_file_gaussian.out(或.log),使用MView或GaussView即可查看对应的扫描结果。可以看出3-氯吡啶与 \(CO_{2}\) 大约在间距为 3.8 Å时能量最低,结合能约为 0.1 kcal/mol。
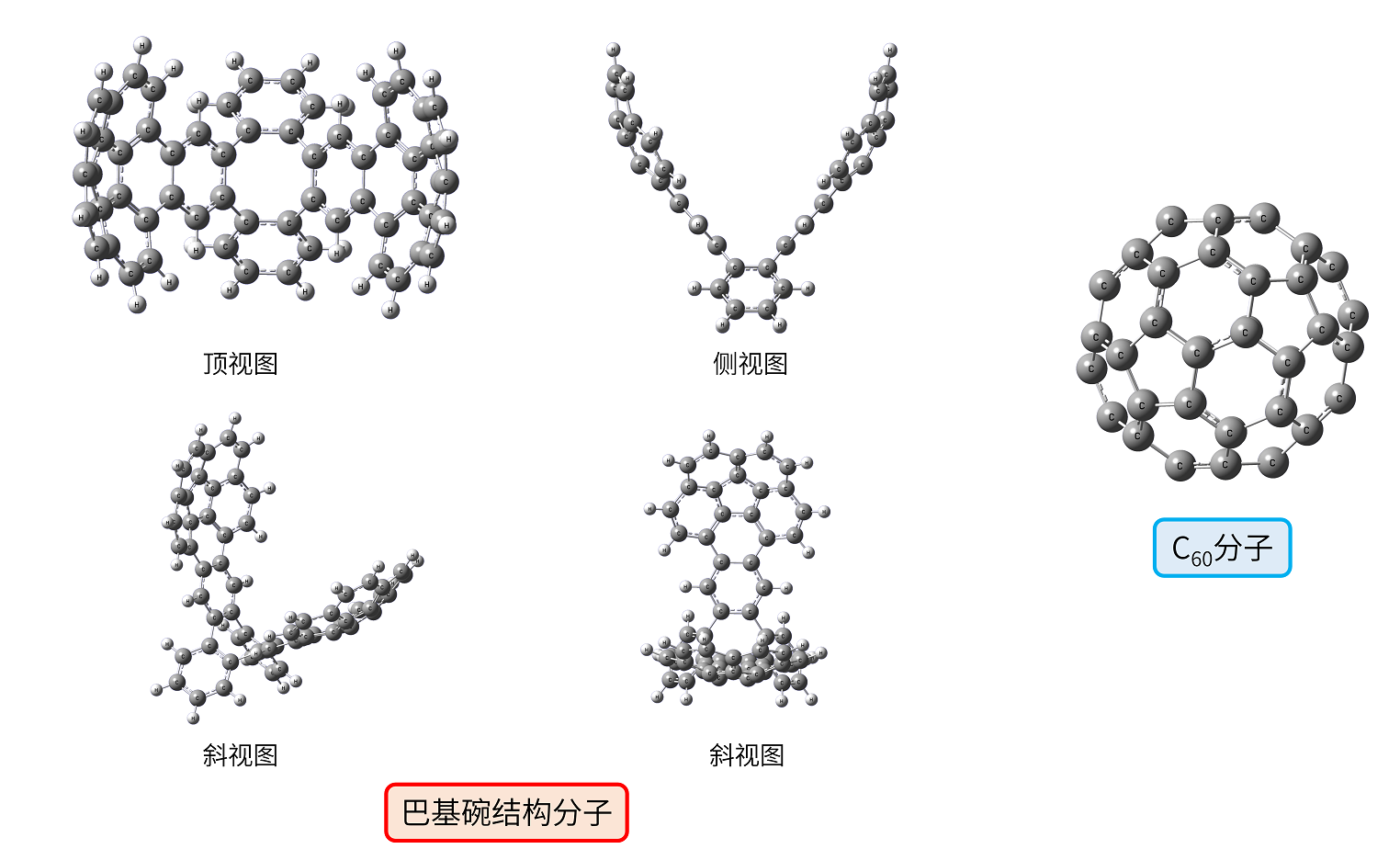
10.2 \(C_{60}\) 与巴基碗结构的 \(\pi\) - \(\pi\) 相互作用
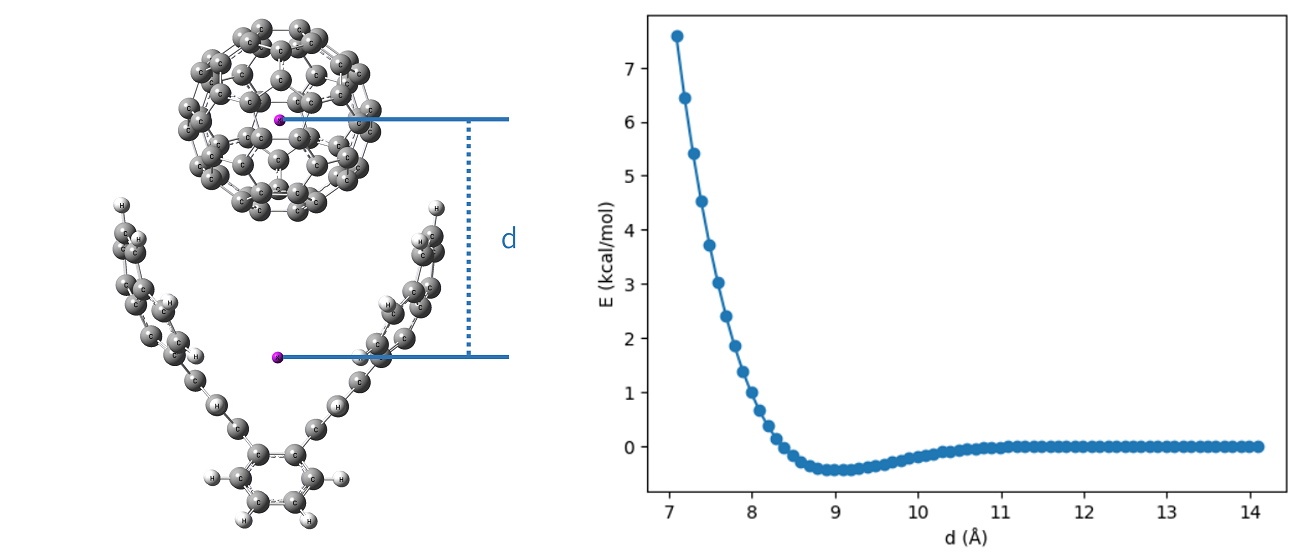
\(C_{60}\) 俗称 “富勒烯” 或 “足球烯”,是由60个碳原子构成的类似足球的空心球体,这个球体由12个正五边形和20个正六边形拼接而成,结构非常对称和完美。它于1985年被发现,并在1996年获得了诺贝尔化学奖,是纳米科技领域的里程碑式发现,至今仍是化学研究的明星分子。巴基碗是一类碗状多环芳烃分子,可以视为包含了富勒烯或碳纳米管碎片的分子,同样具有独特的电子性质。本例将通过计算一个钳形巴基碗结构分子与 \(C_{60}\) 能量与距离的关系,研究两者的相互作用。
步骤如下:
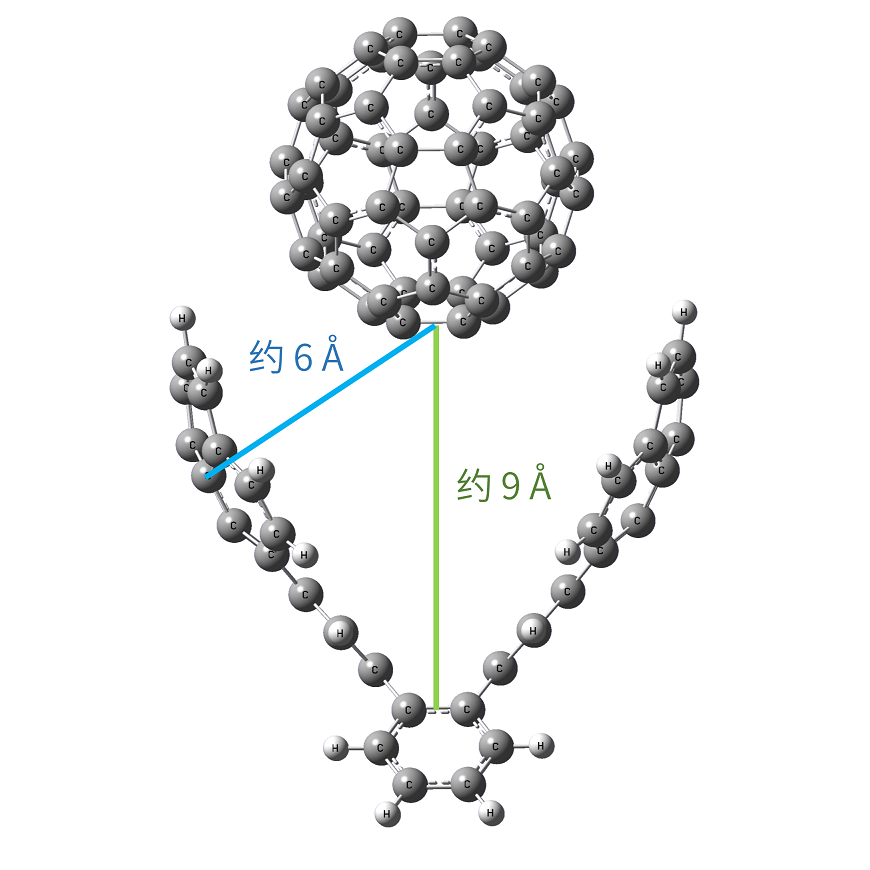
1. 构建钳形巴基碗分子与 \(C_{60}\) 分子结构,使用b3lyp/6-31g(d)将它们进行几何优化后组合起来,对得到的超分子结构再次进行优化,最终得到稳定的复合产物。此时 \(C_{60}\) 与钳形巴基碗结构分子底部距离约为 9 Å,与壁部的距离约为 6 Å。
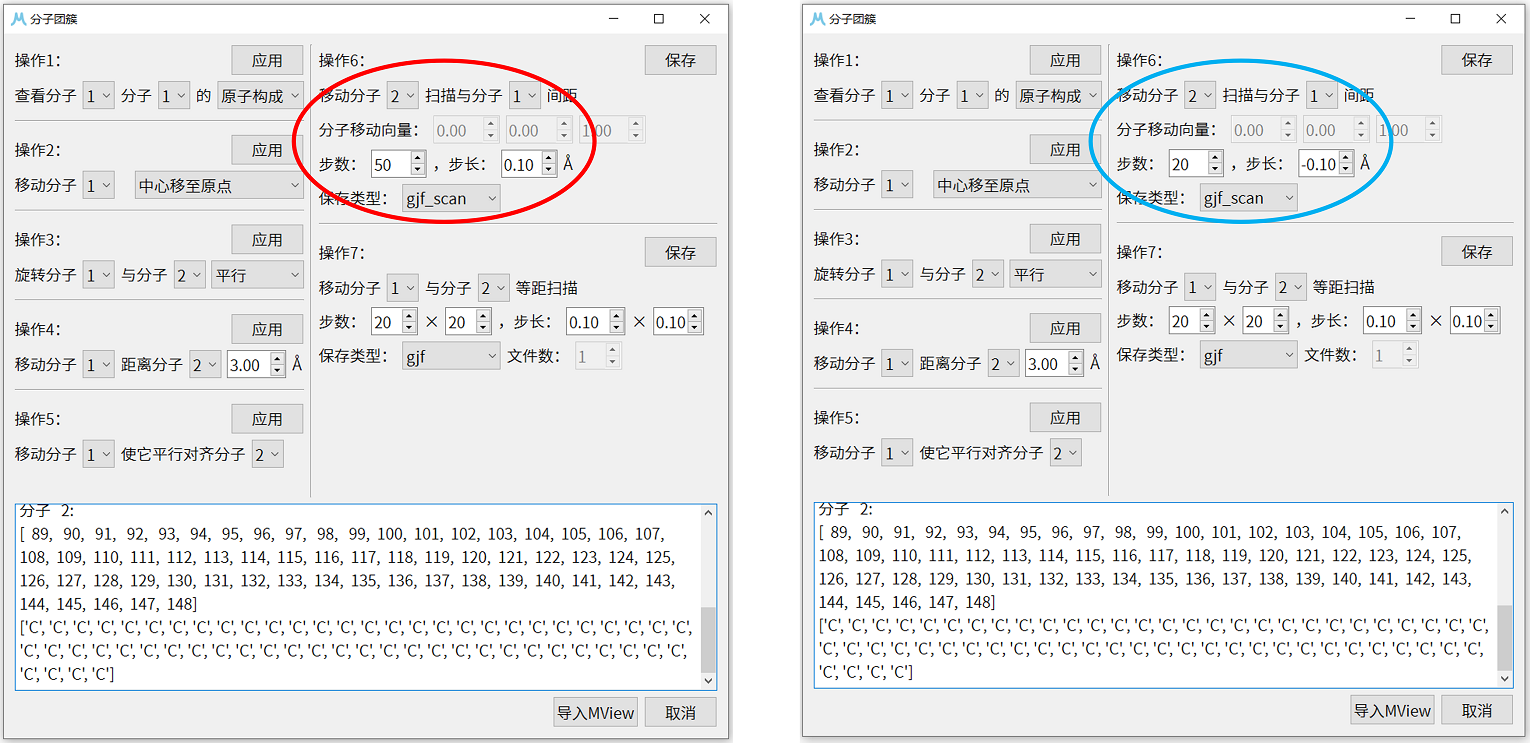
2. 将优化好的复合物超分子结构导入MView中。通过操作1的查看原子组成可知分子1为钳形巴基碗结构分子,分子2为 \(C_{60}\) 分子。使用操作6,选择移动分子2扫描与分子1间距,将扫描步数设为50,步长设为 0.10 Å,保存类型选择gjf_scan,点击保存,选择保存路径后得到 \(C_{60}\) 分子远离钳形巴基碗结构分子的扫描文件。把得到的扫描文件重命名防止覆盖,再将扫描步数设为20,步长设为 -0.10 Å,可以保存得到 \(C_{60}\) 分子靠近钳形巴基碗结构分子的扫描文件。
3. 使用文本编辑器对两个构建好的扫描文件进行微调,扫描方法改为b3lyp/6-31g(d),使用Gaussian对两个文件进行扫描计算,扫描完成后可使用MView或GaussView可对结果进行查看,也可以把扫描结果数据导出后拼接,得到完整的扫描文件。
10.3 使用ORCA对两个苯分子进行等距扫描
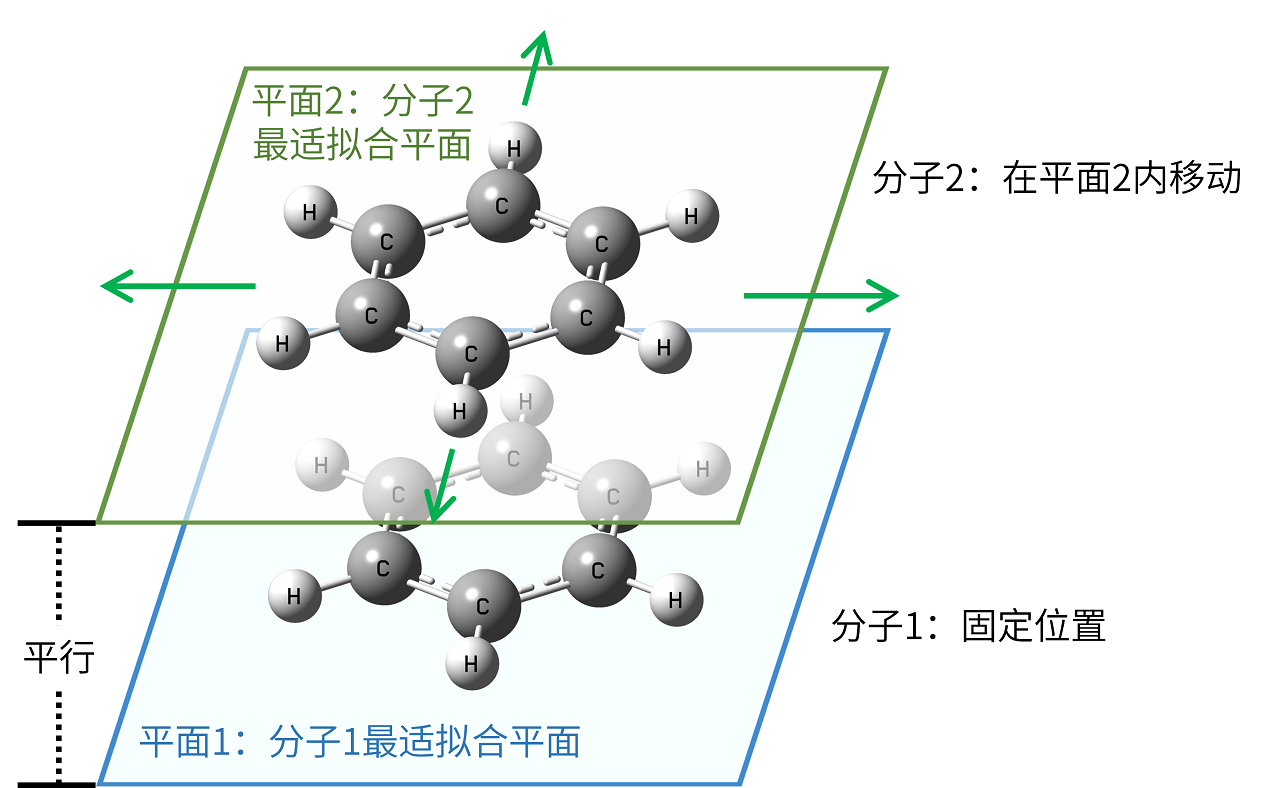
苯分子间的弱相互作用是典型的 \(\pi\) - \(\pi\) 相互作用。对于两个苯分子,无论它们的苯环平面是平行还是垂直,均存在 \(\pi\) - \(\pi\) 相互作用。本例将使用ORCA软件研究两个苯环平面平行且保持特定平面间距离时,体系能量随苯分子位置变化的变化情况,并对比B3LYP/6-31G与wB97X-V/def2-TZVP两种方法的结果。
步骤如下:
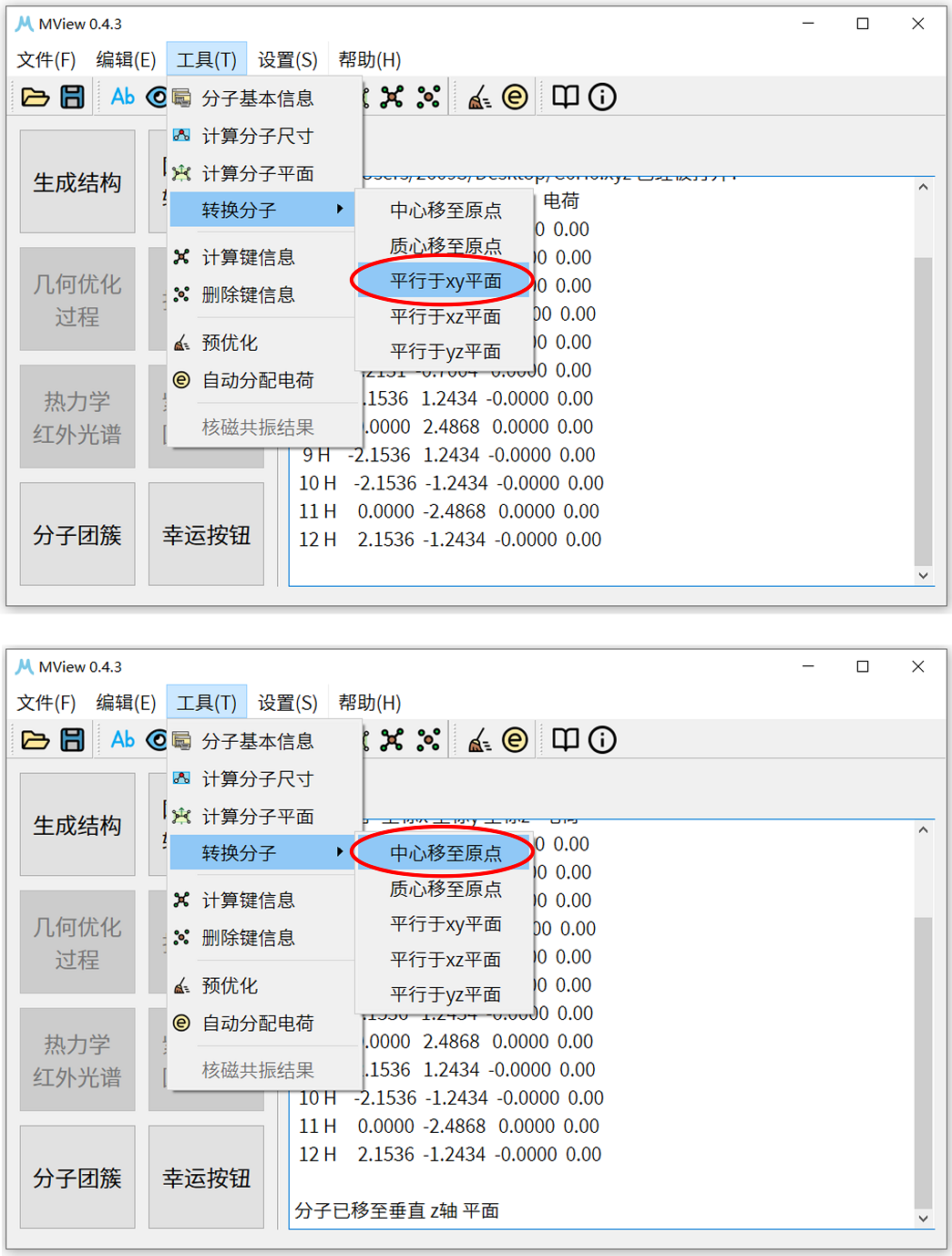
1. 首先尝试B3LYP/6-31G方法。先使用其它可视化软件构建出苯分子。将得到的分子结构文件拖入MView中,点击工具-转换分子-平行于xy平面,将分子转换至平行于xy平面方向。再点击工具-转换分子-中心移至原点,这一系列操作是将分子转换至坐标系中央, 并尽可能处于坐标系xy平面,这样可以方便优化后超分子的构建。
2. 点击保存按钮,选择Orca input格式,得到ORCA输入文件。修改计算任务、计算方法等基本参数,使用ORCA软件进行优化,得到优化后的.xyz文件。
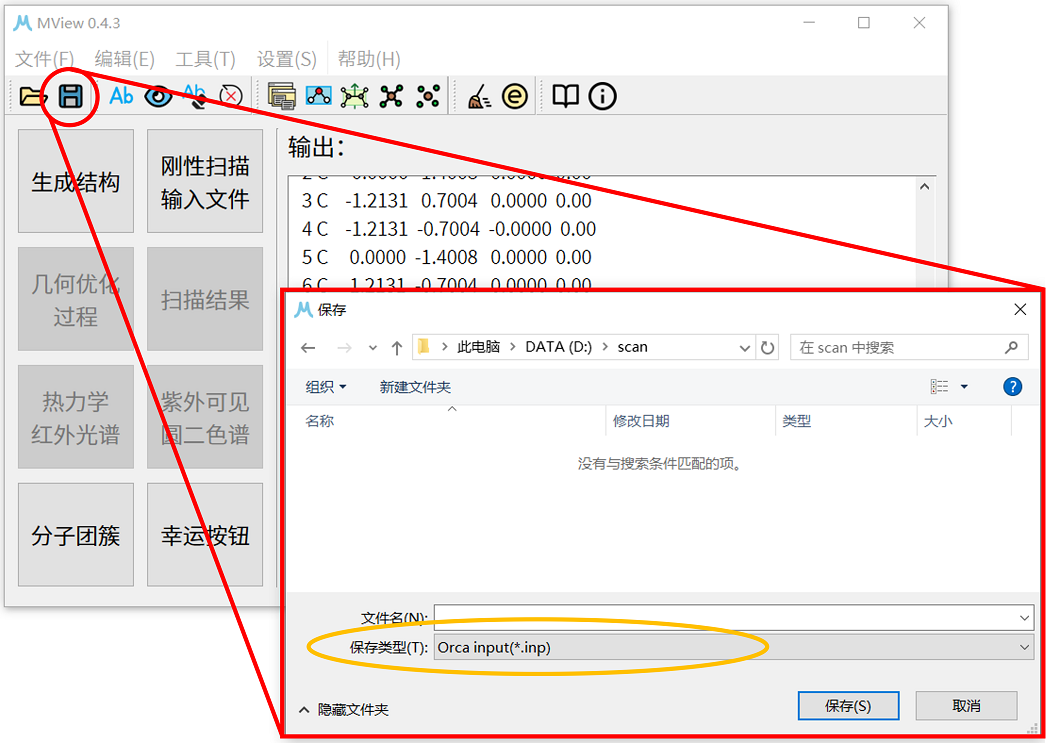
3. 将得到的.xyz文件拖入MView中,点击工具栏中的显示坐标按钮,如果此时分子所有原子的z坐标为0,则此步可跳过。否则重复步骤1的操作,并将新结构重新保存为.xyz文件。现在的苯分子位于坐标系的xy平面,且中心与坐标系原点重合。
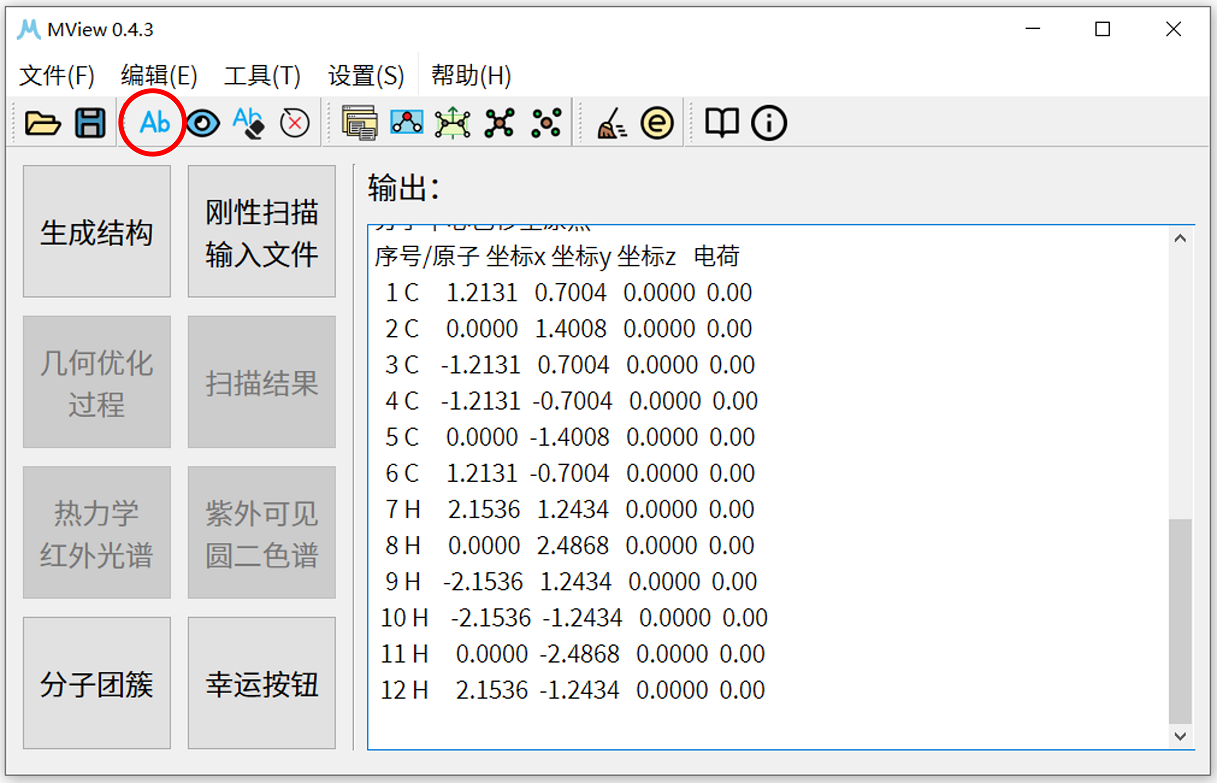
4. 使用记事本或其它文本编辑工具打开.xyz文件,将第一行的原子数由12改为24,并复制后面所有原子的信息,复制后粘贴至文件末尾,并将所有粘贴的原子的原子坐标z值改为3.5。保存文件。此时已经得到了两个间距为 3.5 Å的苯分子文件,设置为 3.5 Å是由于苯分子的 \(\pi\) - \(\pi\) 相互作用典型距离为 3.0-4.0 Å。除本例介绍的方法外,读者也可以使用类似10.1节案例中的方法构建对应的苯超分子结构文件。
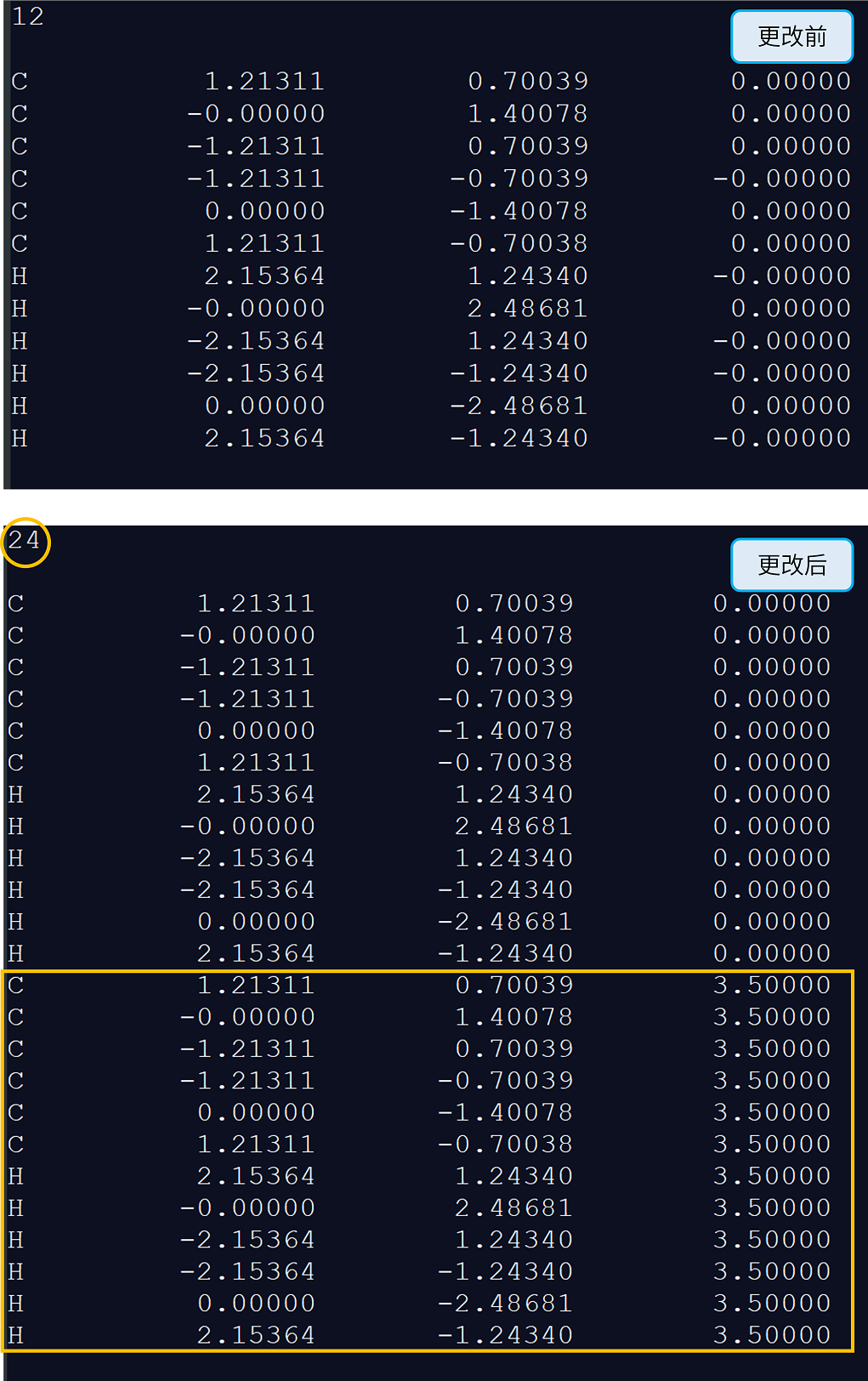
5. 将现在的.xyz文件拖入MView中,点击工具栏中的添加键信息按钮,为超分子添加键信息。
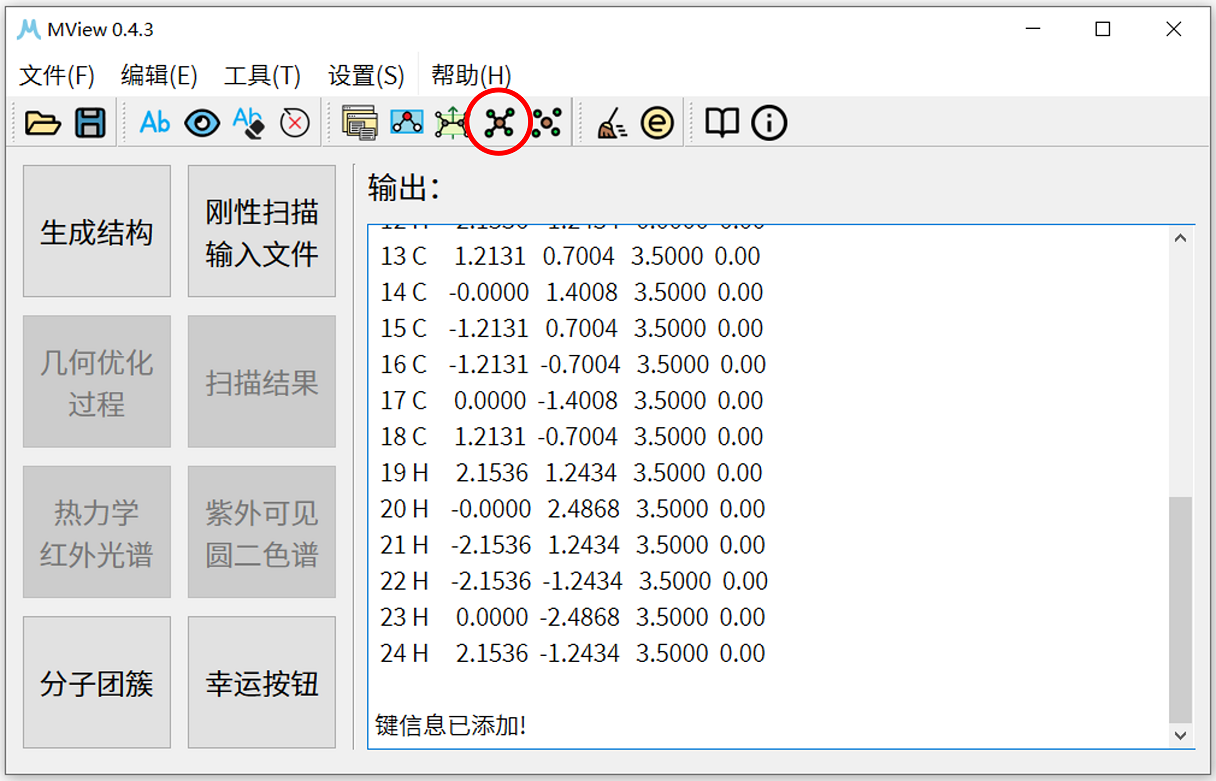
6. 点击分子团簇按钮进入分子团簇页面,在操作7中选择移动分子2与分子1等距扫描,扫描步数设置为50×50,步长设置为0.10×0.10,保存类型选择xyz_orca,文件数设置为5。点击保存,选择要保存的文件夹位置,得到scan_file_1.xyz到scan_file_5.xyz 5个.xyz文件。这里的文件数是保存文件的数目,它会根据扫描结构数量尽可能将结构平均的保存到每个文件中,例如本例会有2500个扫描结构,保存后得到的5个.xyz文件将各包含500个结构。后续使用ORCA进行扫描时,可以同时投入5个任务进行计算,缩减计算时间。
7. 使用ORCA分别对5个.xyz文件进行单点能计算,泛函与基组设置为B3LYP/6-31G。计算完成后会得到5个.out文件,将5个文件依序进行拼接,最终得到一个总的.out文件。
8. 将总的.out文件拖入MView中,点击扫描结果按钮,弹出扫描窗口,在弹出的窗口中点击2D,并在下拉框中选择50×50,即可可视化势能面扫描结果。
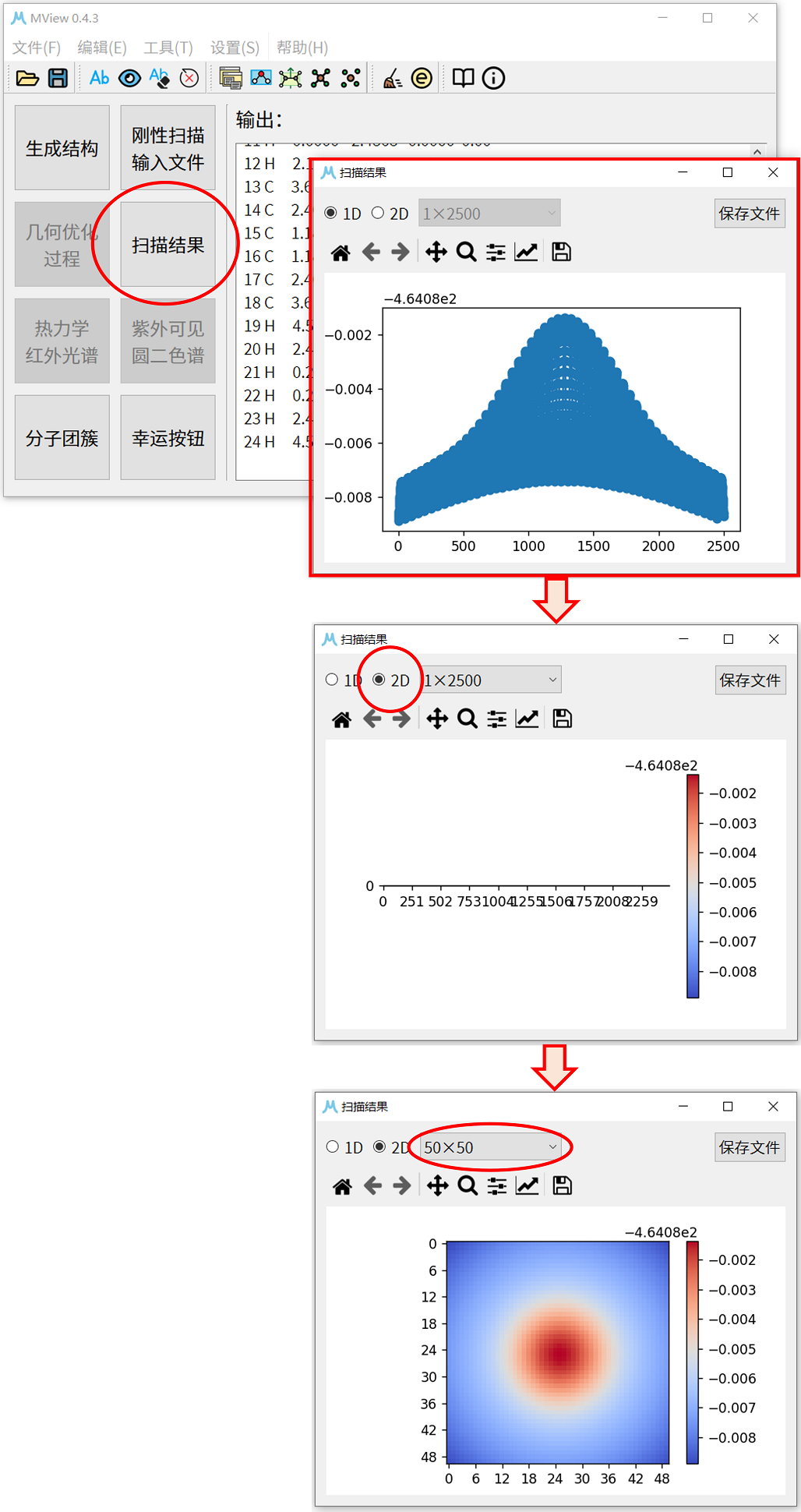
9. 分析得到的结果,可以看到当两个苯环完全对齐时,体系能量最高,两个苯间离得越远,体系能量越低。显然,B3LYP方法未能合适的描述苯环间的 \(\pi\) - \(\pi\) 相互作用。重复本例前面的操作,同时将计算方法与基组更换为wB97X-V/def2-TZVP,得到下图结果。
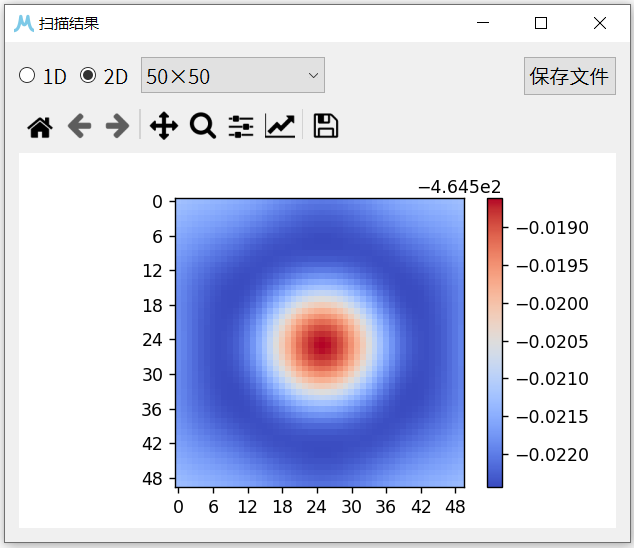
wB97X-V方法得到的势能面显示,在两个苯环完全对齐时,体系能量较高,当两个苯环交错排列时,体系能量最低,苯环间存在吸引作用,该结果与通常认知的 \(\pi\) - \(\pi\) 相互作用是一致的。